50 divide and conquer interview questions [easy, medium, hard]

To ace your coding interview for a software engineering job, you’ll need to understand divide and conquer. It is a problem solving approach that divides a problem into smaller subproblems that are easier to solve, then combines the subproblem solutions into the solution for the original problem. Divide and conquer comes up frequently in coding interviews and is fundamental to many other algorithms such as binary search and mergesort.

Let’s take a look at some typical divide and conquer questions.

Below, we take a look at 50 divide and conquer questions and provide you with links to high quality solutions to them. 

This is an overview of what we’ll cover:

1. Easy divide and conquer interview questions
2. Medium divide and conquer interview questions
3. Hard divide and conquer interview questions
4. Divide and conquer basics
5. Divide and conquer cheat sheet
6. How to prepare for a coding interview

Let's get started.

Click here to practice coding interviews with ex-FAANG interviewers

1. Easy divide and conquer interview questions

You might be tempted to try to read all of the possible questions and memorize the solutions, but this is not feasible. Interviewers will always try to find new questions, or ones that are not available online. Instead, you should use these questions to practice the fundamental concepts of divide and conquer.

As you consider each question, try to replicate the conditions you’ll encounter in your interview. Begin by writing your own solution without external resources in a fixed amount of time.

If you get stuck, go ahead and look at the solution, but then try the next one alone again. Don’t get stuck in a loop of reading as many solutions as possible! We’ve analysed dozens of questions and selected ones that are commonly asked and have clear and high quality answers.

Here are some of the easiest questions you might get asked in a coding interview. These questions are often asked during the “phone screen” stage, so you should be comfortable answering them without being able to write code or use a whiteboard.

2. Medium divide and conquer interview questions

Here are some moderate-level questions that are often asked in a video call or onsite interview. You should be prepared to write code or sketch out the solutions on a whiteboard if asked.

3. Hard divide and conquer interview questions

Similar to the medium section, these more difficult questions may be asked in an onsite or video call interview. You will likely be given more time if you are expected to create a full solution.

4. Divide and conquer basics

In order to crack questions about divide and conquer, you’ll need to have a strong understanding of the algorithm, how it works, and when to use it.

4.1 What is divide and conquer?

Divide and conquer (DAC) is an algorithmic paradigm used to solve problems by continually dividing the problem into smaller parts until a part is easy enough to solve (conquer) on its own. The solutions to the solved parts are then combined to give the solution for the original problem. For optimization problems, being able to build an optimal solution based on the optimal solution of smaller parts is known as an optimal substructure.

Let’s solve an accumulation count problem using DAC. Suppose we are given the following list of musical notes and need to establish how many times each note appears in the list.

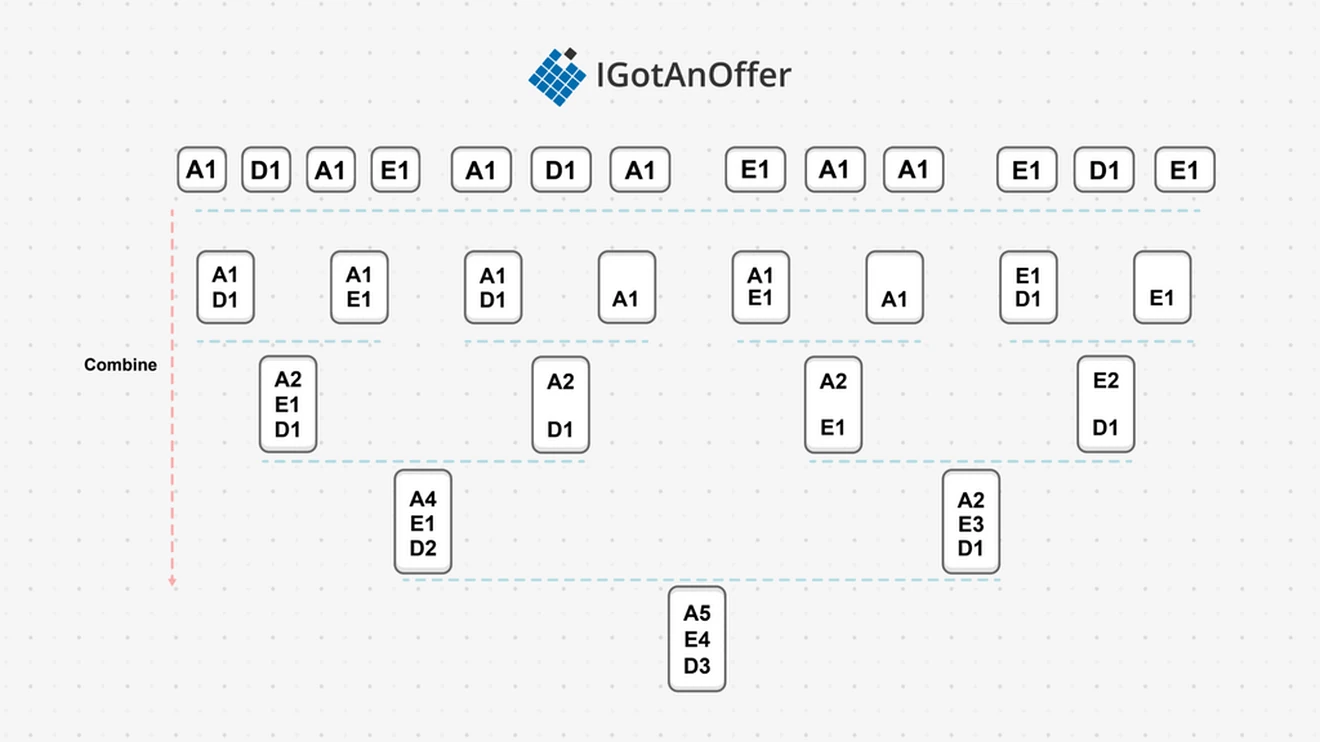
The simplest solution is to use a serial approach to build a frequency table while looping over the list. The DAC approach instead divides the list into two recursively until only one note is left in each sublist, and then returns the frequency table for the one note only, illustrated by the conquer layer in the diagram.

In the next step, the one-note tables are combined in the reverse of the divide action, then those combined tables are combined again, and so it continues until one big table is formed with the note count for the entire list. Combining two tables means adding them together, so combining the A1;D1 table to the A1;E1 table gives us the A2;E1;D1 table.

The benefit this offers over the serial solution is that the sub-problems can be solved in parallel. In summary, a DAC algorithm will consist of the following steps:

1. Divide – the problem is divided into two or more smaller sub-problems in a serial fashion using recursion.
2. Conquer – each sub-problem is solved serially or in parallel.
3. Combine – the solutions of the sub-problems are combined in a serial fashion.

4.1.1 Use cases for divide and conquer

Most problems and operations using lists can be solved using DAC, but some problems not related to lists can also be solved using DAC:

• Sorting – both Mergesort and Quicksort are DAC implementations
• Finding the maximum and/or smallest element in a list
• Strassen’s matrix multiplication algorithm
• Karatsuba’s multiplication algorithm
• Cooley-Tukey’s fast Fourier transform algorithm
• Solving the nth Fibonacci number
• Finding the closest pair of points in a matrix

4.1.2 Example implementation

Since DACs are recursive functions, they require at least one base condition which is followed by the divide, conquer, and combine steps. For our frequency count problem, this results in the following implementation:

The base condition stops the recursion when the array only has one note, and will return the frequency table for this single note. Next, the algorithm divides the list into two sublists, and conquers each sublist separately. The results of the two sublists are finally combined into one table which is returned.

4.1.3 How divide and conquer compares to other algorithms

Decrease-and-conquer algorithms are similar to DACs in that they also reduce problems into smaller sub-problems that are easier to solve. However, decrease-and-conquer algorithms will only focus on one of the sub-problems and discard the others. A classic example is binary searching, which divides a list into two but will only continue searching in one of the two sublists. A DAC on the other hand always conquers two or more sub-problems.

Dynamic programming can also be applied to problems with optimal substructures when they have overlapping sub-problems. An example of this is finding the nth Fibonacci number, which is a problem that has an optimal substructure (because it requires finding the n-1 and n-2 Fibonacci number) and has overlapping sub-problems (since finding n-1 will again find n-2). Here, dynamic programming will solve the problem in polynomial time while DAC will take exponential time.

Greedy algorithms can be applied to problems with optimal substructure that also have the greedy property. The greedy property guarantees the optimal solution of sub-problems will result in the optimal solution of the global problem. Few problems have this property and proving a solution makes use of it is tricky, but when a greedy algorithm can be used, the average run time can be better.

MapReduce is a programming paradigm that is an example of DAC. First data is mapped or divided into components, and then reduced or "conquered" to the desired solution. Hadoop is a framework that implements the MapReduce paradigm and allows for massive parallelism on big data.

5. Divide and conquer cheat sheet

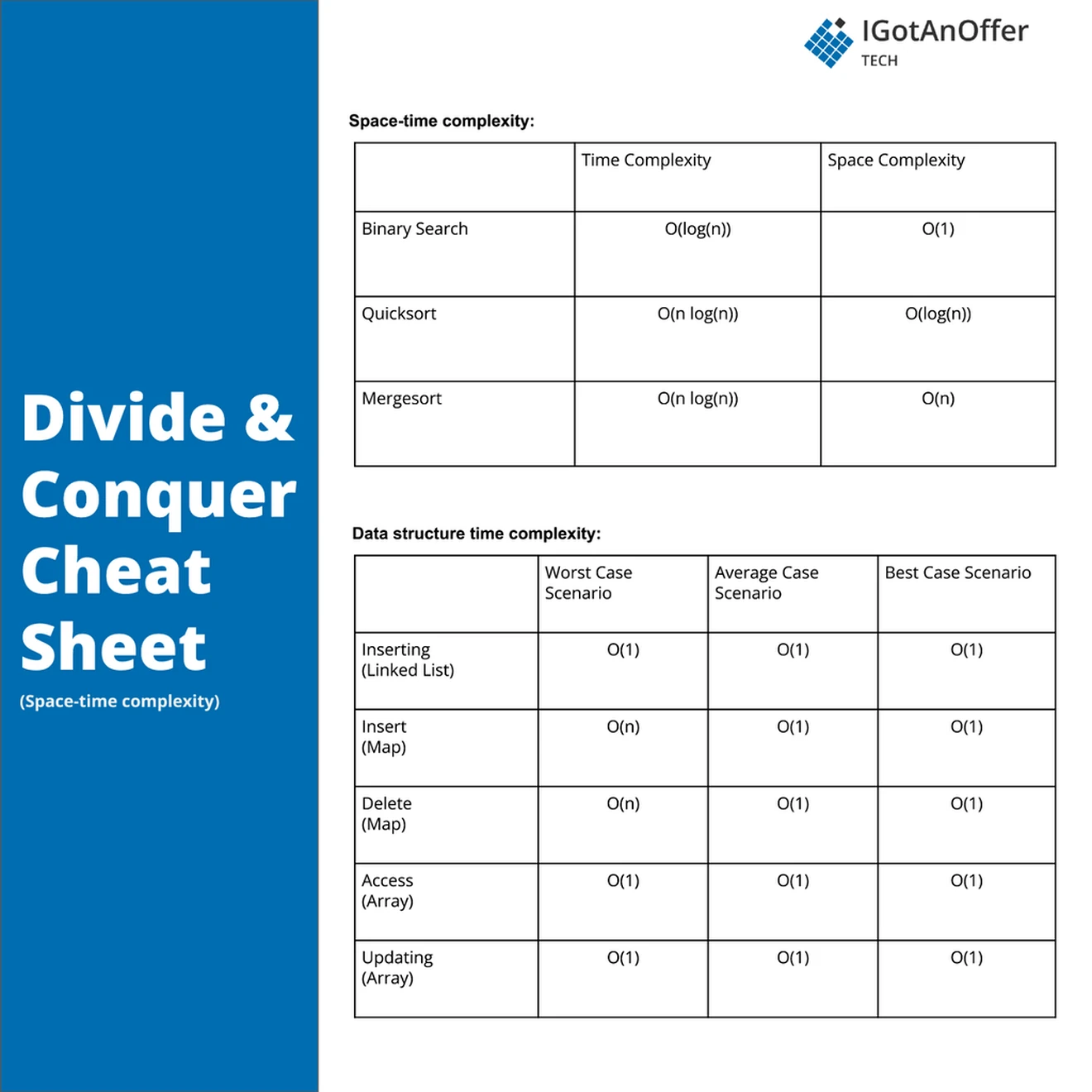
You can download the cheat sheet here.

5.1 Related algorithms and techniques

• Cooley-Tukey algorithm

• Strassen algorithm

• Karatsuba algorithm

5.2 Cheat sheet explained

The cheat sheet above is a summary of information you might need to know for an interview, but it’s usually not enough to simply memorize it. Instead, aim to understand each result so that you can give the answer in context.

The cheat sheet is broken into time complexity and space complexity (the processing time and memory requirements for divide and conquer). Divide and conquer is related to several data structures, which are also included in the cheat sheet.

For more information about time and space requirements of different algorithms, read our complete guide to big-O notation and complexity analysis.

5.2.1 Time complexity

In our frequency problem, the list is divided in two for a total of log_2(n) + 1 divide and combine iterations. Each combine operation only loops over half the elements (n/2) at each iteration to give a total time complexity of O(n log_2(n)). The serial solution is better at linear time, but cannot run in parallel like the DAC solution does. Not all problems solved with a DAC algorithm have a serial solution too, however.

In the general case, a DAC algorithm will take more than linear time but less than exponential time, like brute forcing. Mergesort and Quicksort illustrate this: Mergesort worst-case time complexity is O(n log(n)) and Quicksort O(n^2), but both have an average-case time complexity of O(n log(n)).

5.2.2 Space complexity

The only extra space used by our divide-and-conquer algorithm is the frequency table. In the worst case, each element only appears once, and the table will need an entry for every element, giving a space complexity of O(n). The serial solution would use the same table to keep track of the frequency of notes.

In general, the space complexity is not the same for all DAC algorithms. For example, the space complexity of Mergesort is O(n), while that of Quicksort is O(log n).

5.2.3 Related algorithms and data structures: maps and lists

Almost any data structure is used across the various DAC implementations to problems. For our note-frequency problem we used a map, which offers constant insertion and updating times. Mergesort uses a list, but only adds to the end of the list when merging, to achieve constant time insertions. Quicksort does not use any extra data structures but moves items on the list it is operating on, with each move having a time complexity of O(n) in the worst case.

6. How to prepare for a coding interview

6.1 Practice on your own

Before you start practicing interviews, you’ll want to make sure you have a strong understanding of not only divide and conquer but also the rest of the relevant algorithms and data structures. You’ll also want to start working through lots of coding problems.

Check out the guides below for lists of questions organized by difficulty level, links to high-quality answers, and cheat sheets.

Algorithm guides

• Depth-first search
• Breadth-first search
• Binary search
• Sorting
• Dynamic programming
• Greedy algorithm
• Backtracking

Data structure guides

• Arrays
• Strings
• Linked lists
• Stacks and Queues
• Trees
• Graphs
• Maps
• Heap
• Coding interview examples (with solutions)

To get used to an interview situation, where you’ll have to code on a whiteboard, we recommend solving the problems in the guides above on a piece of paper or google doc.

6.2 Practice with others

However, sooner or later you’re probably going to want some expert interventions and feedback to really improve your coding interview skills.

That’s why we recommend practicing with ex-interviewers from top tech companies. If you know a software engineer who has experience running interviews at a big tech company, then that's fantastic. But for most of us, it's tough to find the right connections to make this happen. And it might also be difficult to practice multiple hours with that person unless you know them really well.

Here's the good news. We've already made the connections for you. We’ve created a coaching service where you can practice 1-on-1 with ex-interviewers from leading tech companies. Learn more and start scheduling sessions today.