50+ depth-first search (DFS) interview questions [easy, medium, hard]

To ace your coding interview for a software engineering job, you’ll need to understand depth-first search. It comes up frequently in coding interviews and is fundamental to many other algorithms too.

Let’s take a look at some typical depth-first search questions.

Below, we take a look at 50 more depth-first search questions and provide you with links to high quality solutions to them. 

This is an overview of what we’ll cover:

1. Easy depth-first search interview questions
   
2. Medium depth-first search interview questions
3. Hard depth-first search interview questions
4. Depth-first search basics
5. Depth-first search cheat sheet
6. How to prepare for a coding interview

Let's get started.

Click here to practice coding interviews with ex-FAANG interviewers

1. Easy depth-first search interview questions

You might be tempted to try to read all of the possible questions and memorize the solutions, but this is not feasible. Interviewers will always try to find new questions, or ones that are not available online. Instead, you should use these questions to practice the fundamental concepts of depth-first search.

As you consider each question, try to replicate the conditions you’ll encounter in your interview. Begin by writing your own solution without external resources in a fixed amount of time.

If you get stuck, go ahead and look at the solution, but then try the next one alone again. Don’t get stuck in a loop of reading as many solutions as possible! We’ve analysed dozens of questions and selected ones that are commonly asked and have clear and high quality answers.

Here are some of the easiest questions you might get asked in a coding interview. These questions are often asked during the “phone screen” stage, so you should be comfortable answering them without being able to write code or use a whiteboard.

2. Medium depth-first search interview questions

Here are some moderate-level questions that are often asked in a video call or onsite interview. You should be prepared to write code or sketch out the solutions on a whiteboard if asked.

3. Hard depth-first search interview questions

Similar to the medium section, these more difficult questions may be asked in an onsite or video call interview. You will likely be given more time if you are expected to create a full solution.

4. Depth-first search basics

In order to crack questions about depth-first search, you’ll need to have a strong understanding of the algorithm, how it works, and when to use it.

4.1 What is depth-first search?

We can categorize all data structures into two categories: Those with a simple option for visiting each item, and those with multiple, complex options for visiting each item. Data structures like arrays, list, stacks, and queues fall in the first category – we can easily visit each node in an array by traversing over the array indices; following each link for a list; popping from a stack; and dequeuing from a queue. But for a tree or graph data structure, it is not so simple.

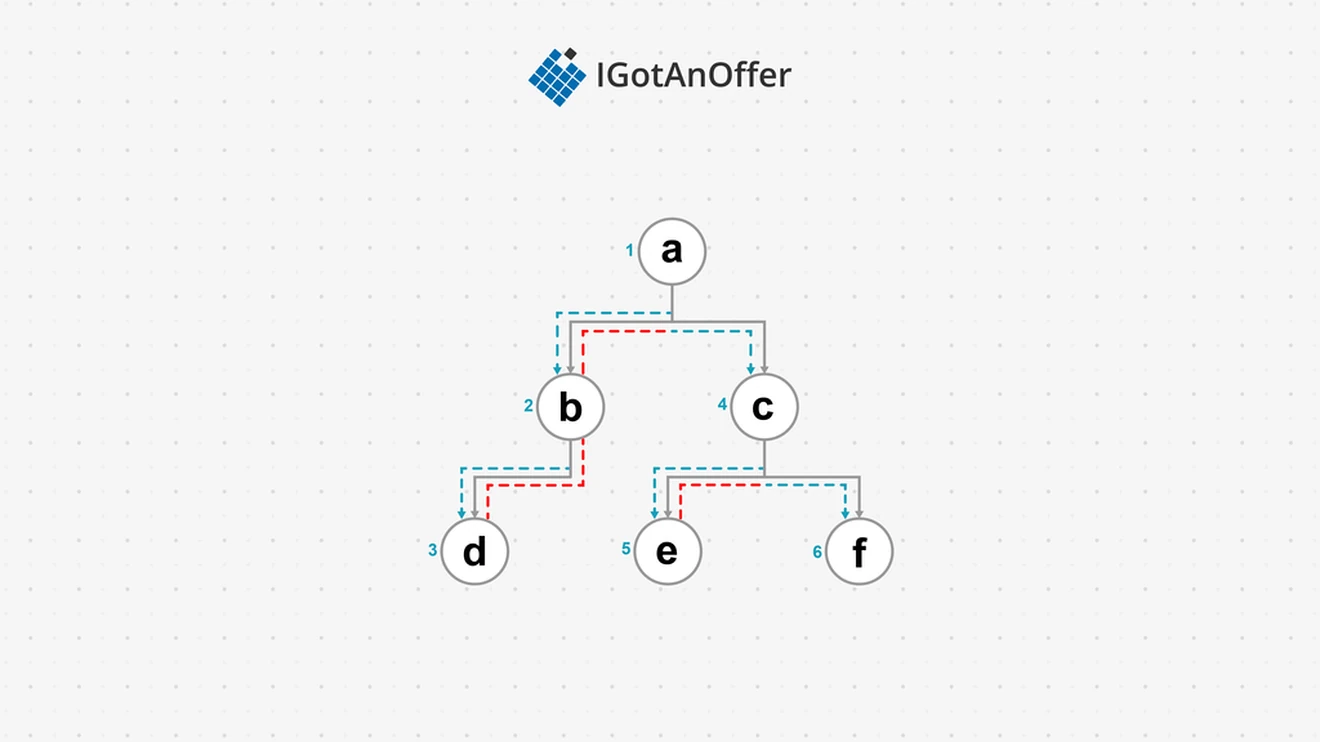
A depth-first search (or traversal) is an option for visiting all the nodes in a tree or graph. In a depth-first search (DFS), we visit child nodes first before siblings. For example, in the tree below, we start at the root node a and then go to its first child b, then b’s child d. Only after this do we go back up to visit c. So the visit order is abdcef for this tree.

4.1.1 Use cases for depth-first search (Java, Python, C++)

There are many instances when we need to visit the nodes in a tree or graph. Some include:

• Printing out the elements in a tree representing a mathematical expression.
• Determining if one node can be reached from another node in a directed or undirected graph of a social network or cities.
• Creating a topological sorting of tasks in a Gantt chart (directed graph) to ensure they are completed in an order that respects dependencies.
• Solving a puzzle with a single solution like a maze. However, DFS won't find the best solution if multiple solutions exist.
• Detecting whether a directed graph has cycles as part of a static-analysis for multi-threaded code with mutex locks to ensure the code is deadlock free.
• Testing properties of a graph like bipartite, biconnectivity, strongly connected, etc.

4.1.2 Example implementation

The simplest implementation is for a tree data structure. Here we start our DFS with the root node and then iterate over its children. With each iteration we make a recursive call to the DFS using the current child.

Tree DFS

Depth-first traversal for binary trees has three variations: In-order, pre-order, and post-order traversal. These refer to the order in which a node and its child nodes are visited. In-order traversal visits the node's left subtree, then the parent node, then the right subtree, i.e. the node is visited between its children. Pre-order traversal visits the node first, then the left subtree, then the right subtree, i.e. the node is visited before its children. Post-order traversal visits the left subtree, then the right subtree, and finally the node, i.e. visiting the node after the children.

The tree algorithm is not suitable for graphs however. Consider the following three graphs:

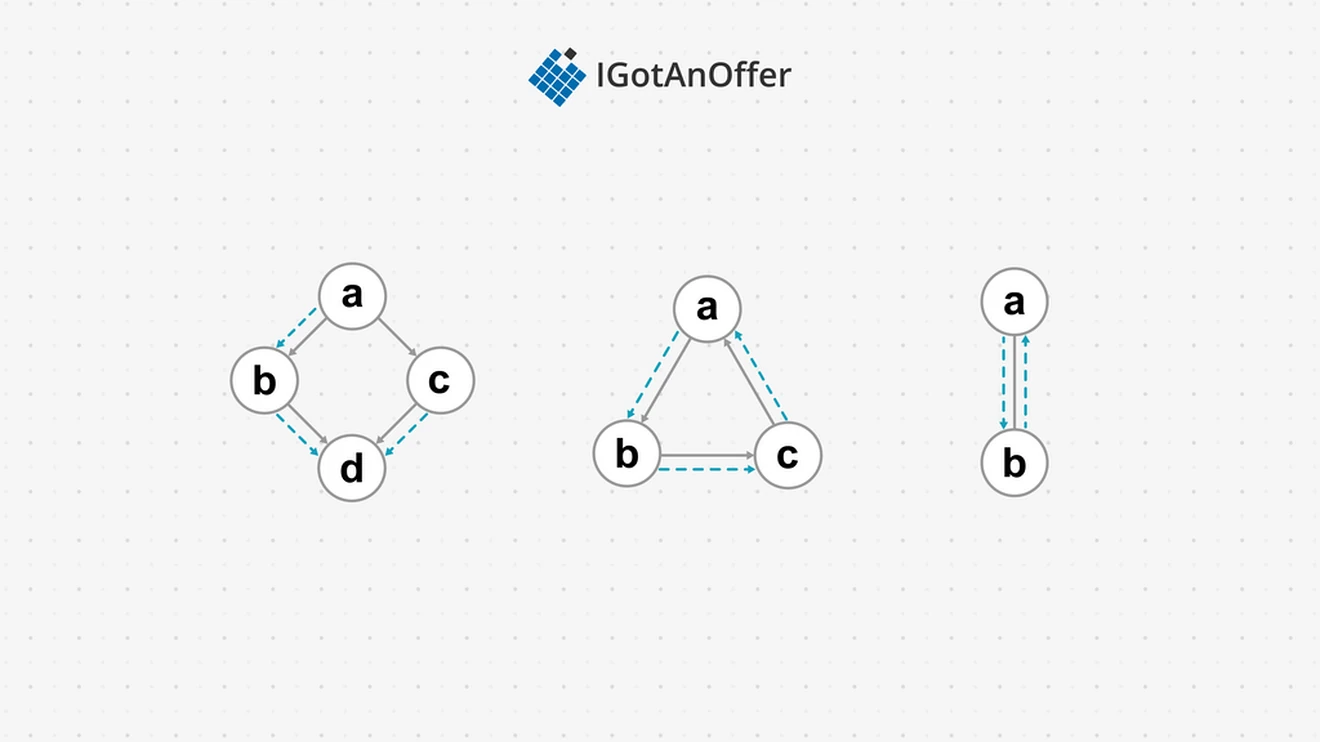
In the first graph, the tree DFS will visit abd and then go back to c to visit cd, resulting in d being visited twice. In the second graph, the algorithm will visit the nodes abc in an infinite loop. In the last undirected graph, ab will be visited repeatedly.

The solution is to keep track of the nodes that have already been visited, and skip visiting them if they are encountered again. Here is an implementation using a visited list:

Graph DFS

Using this algorithm on the three earlier graphs will work as expected. With the first graph, abd will be visited first, and then the algorithm will move to c. When d is reached for the second time, the check to see if the node is not in the visited list will return false, thereby skipping the code for printing the node and visiting its children. The final output will be abdc. 

In the second graph, abc will be visited, but attempting to follow the edge from c to a will also result in the visited node check preventing a being visited twice. Likewise, in the final graph ab will be visited, but the visited list check will prevent the algorithm from returning to a again. 

For disjoint graphs (the union of two or more distinct and disconnected graphs), another tweak to the algorithm is needed.

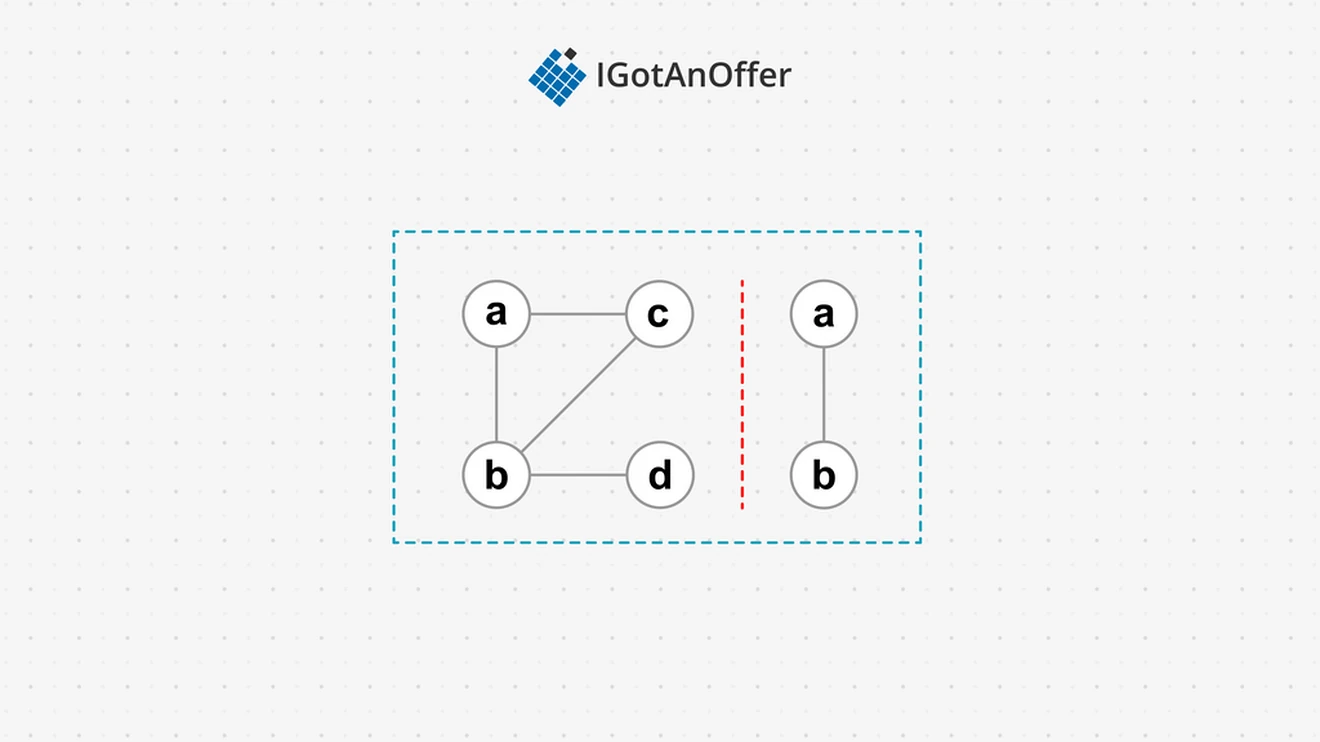
If traversal starts with any of the vertices in the left subgraph – i.e. a, b, c, or d – then the vertices in the right subgraph – i.e. e and f – will never be visited, since there are no links to them. The same applies should traversal start with any vertex on the right subgraph; vertices on the left subgraph will not be visited. To resolve this, a DFS can be started from every node in the disjoint graph, by adding an outer function which starts a DFS for every node in the disjoint graph.

Graph DFS complete

This loop in dfs starts the algorithm for some vertex in each subgraph, ensuring the entire graph is visited.

4.1.3 How depth-first search compares to other algorithms

For graphs and trees, breadth-first search (BFS) is an alternative for visiting all the nodes. Internally, DFS uses a stack (sometimes implicitly, as with this recursive implementation) whereas BFS uses a queue. 

In some cases, DFS can have performance issues compared to BFS. For example, in a tree with many more nodes in its left branch than its right branch, a DFS will exhaustively search the left branch before starting to search the right branch. This isn’t ideal if the solution being searched for happens to be near the top of the right branch. Breadth-first search can perform better in such cases, as it searches level by level, instead of branch by branch. 

The tree implementation of DFS (without a visited node list) has an advantage over BFS in that it uses less memory: only the current visit path is stored in the stack. In contrast, BFS keeps track of all the nodes to visit next in its queue. When a visited node list is used in DFS, the memory usage of a DFS can be greater than that of a BFS, as eventually all nodes are recorded in the visited list.

DFS can have a height limit set into the implementation to stop it from getting stuck in deep branches. When this limit is made iterative from 0 until a solution is found (called an iterative DFS), then a space-efficient hybrid is created between DFS and BFS.

Backtracking is a specialized DFS that offers better time and space performance for solution space searching. This is achieved by abandoning early those search paths that have been determined will not have the solution being searched for.

5. Depth-first search cheat sheet

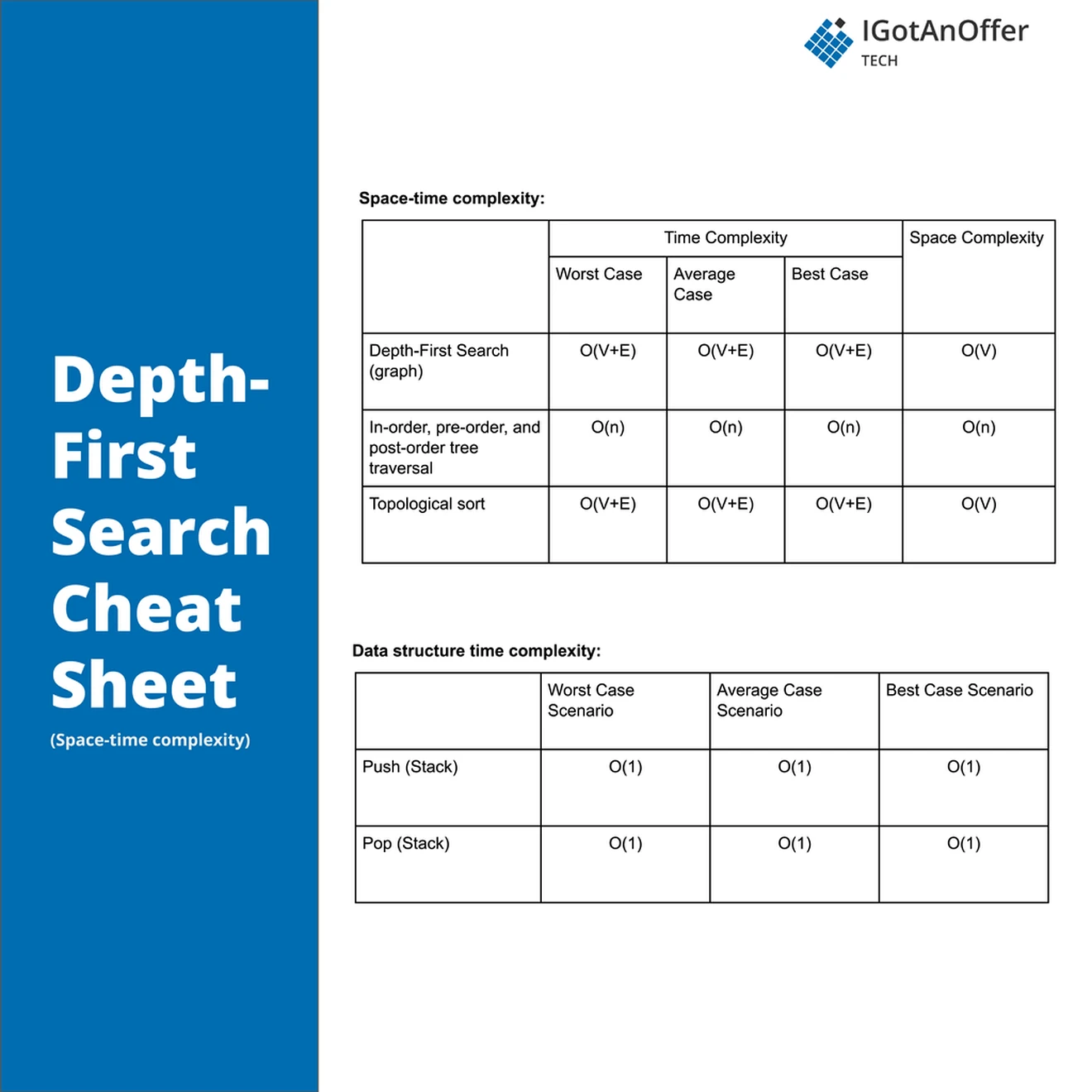
You can download the cheat sheet here.

5.1 Related algorithms and techniques

• Bipartite/bi-graph
• Topological sort
• Morris traversal
• Tree traversal
• Eulerian path

5.2 Cheat sheet explained

The cheat sheet above is a summary of information you might need to know for an interview, but it’s usually not enough to simply memorize it. Instead, aim to understand each result so that you can give the answer in context.

The cheat sheet is broken into time complexity and space complexity (the processing time and memory requirements for depth-first search). Depth-first search is related to several data structures, which are also included in the cheat sheet.

For more information about time and space requirements of different algorithms, read our complete guide to big-O notation and complexity analysis.

5.2.1 Time complexity

For a general graph, DFS visits each vertex and follows each edge to give a time complexity of O(V + E).

For a binary tree, there are a fixed number of edges per node, which give a complexity generally expressed as O(n), n being the number of nodes.

5.2.2 Space complexity

For executing DFS on a tree, space complexity refers to the size of the stack. This is the maximum height of the tree (the deepest  branch) at O(h). When the tree is degenerate – i.e. each node has only one child – then the tree height will be n. This implies a space complexity of O(n) for a tree.

For a graph, the visited list will hold more data than the stack, as eventually every node will be stored in the visited list, resulting in O(V) space used.

5.2.3 Related algorithms and data structures: topological sorting

Consider the DFS use case of getting an ordered list of tasks from a Gantt chart. This is called topological sorting, in which tasks with no constraints are completed first. For example, in the first graph in the second figure above, let’s consider the vertices as tasks, and the edges as dependencies between the tasks. Before task b can be started, task a (its predecessor) must be completed. Similarly, before d can be completed, its predecessors b and c must be completed.

DFS will start unwinding the recursion stack when a vertex no longer has any edges to follow. In our example, the stack will first start unwinding at d. By keeping track of the vertices at each point the stack unwinds, we can create a topological ordering of the graph. Each of the vertices can be pushed onto another stack topology. At the end of the DFS, by popping all the vertices from the topology stack, we get the topological ordering of the graph, in this example acbd.

Like DFS, a topological sort visits each vertex and edge, giving a time complexity of O(V + E). Our variables visited and topology will both contain all the vertices on completion, giving a space complexity of O(V).

6. How to prepare for a coding interview

6.1 Practice on your own

Before you start practicing interviews, you’ll want to make sure you have a strong understanding of not only depth-first search but also the rest of the relevant algorithms and data structures. You’ll also want to start working through lots of coding problems.

Check out the guides below for lists of questions organized by difficulty level, links to high-quality answers, and cheat sheets.

Algorithm guides

• Breadth-first search
• Binary search
• Sorting
• Dynamic programming
• Greedy algorithm
• Backtracking
• Divide and conquer

Data structure guides

• Arrays
• Strings
• Linked lists
• Stacks and Queues
• Trees
• Graphs
• Maps
• Heap
• Coding interview examples (with solutions)

To get used to an interview situation, where you’ll have to code on a whiteboard, we recommend solving the problems in the guides above on a piece of paper or google doc. 

6.2 Practice with others

However, sooner or later you’re probably going to want some expert interventions and feedback to really improve your coding interview skills.

That’s why we recommend practicing with ex-interviewers from top tech companies. If you know a software engineer who has experience running interviews at a big tech company, then that's fantastic. But for most of us, it's tough to find the right connections to make this happen. And it might also be difficult to practice multiple hours with that person unless you know them really well.

Here's the good news. We've already made the connections for you. We’ve created a coaching service where you can practice 1-on-1 with ex-interviewers from leading tech companies. Learn more and start scheduling sessions today.