53 dynamic programming interview questions [easy, medium, hard]

To ace your coding interview for a software engineering job, you’ll need to understand dynamic programming. Dynamic programming optimizes naive solutions to complex problems that have repeated recursive calls for the same inputs. This is achieved by storing solutions to simpler sub-problems to be used later so that they don’t need to be recalculated.

Let’s take a look at some typical dynamic programming questions.

Below, we take a look at 50 dynamic programming questions and provide you with links to high quality solutions to them. 

This is an overview of what we’ll cover:

1. Easy dynamic programming interview questions
   
2. Medium dynamic programming interview questions
3. Hard dynamic programming interview questions
4. Dynamic programming basics
5. Dynamic programming cheat sheet
6. How to prepare for a coding interview

Let's get started.

Click here to practice coding interviews with ex-FAANG interviewers

1. Easy dynamic programming interview questions

You might be tempted to try to read all of the possible questions and memorize the solutions, but this is not feasible. Interviewers will always try to find new questions, or ones that are not available online. Instead, you should use these questions to practice the fundamental concepts of dynamic programming.

As you consider each question, try to replicate the conditions you’ll encounter in your interview. Begin by writing your own solution without external resources in a fixed amount of time.

If you get stuck, go ahead and look at the solution, but then try the next one alone again. Don’t get stuck in a loop of reading as many solutions as possible! We’ve analysed dozens of questions and selected ones that are commonly asked and have clear and high quality answers.

Here are some of the easiest questions you might get asked in a coding interview. These questions are often asked during the “phone screen” stage, so you should be comfortable answering them without being able to write code or use a whiteboard.

2. Medium dynamic programming interview questions

Here are some moderate-level questions that are often asked in a video call or onsite interview. You should be prepared to write code or sketch out the solutions on a whiteboard if asked.

3. Hard dynamic programming interview questions

Similar to the medium section, these more difficult questions may be asked in an onsite or video call interview. You will likely be given more time if you are expected to create a full solution.

4. Dynamic programming basics

In order to crack questions about dynamic programming, you’ll need to have a strong understanding of the technique, how it works, and when to use it.

4.1 What is dynamic programming?

Dynamic programming is an algorithmic paradigm to create optimal solutions for complex problems by breaking them down into simpler sub-problems that can be solved recursively.

Dynamic programming methods are applicable to problems that have the following two properties:

1. Optimal substructure: the optimal solution builds on the optimal solutions of smaller pieces.
2. Overlapping sub-problems: the broken-down versions of the problem are repeated.

These properties can be seen when implementing a function to find the nth Fibonacci number. The general implementation is as follows, with n == 0 and n == 1 being the base cases:

The problem has an optimal substructure, because to get the 6th Fibonacci number, the 5th and the 4th Fibonacci numbers must first be found. It also has overlapping sub-problems, because the 4th Fibonacci needs to be found to get both the 5th Fibonacci number and the 6th. In fact, to calculate the 6th Fibonacci number, the 2nd Fibonacci number will be calculated five times, giving this implementation an exponential time complexity. This diagram of a call stack for fib(6) demonstrates the inefficiency of using plain recursion to solve our problem:

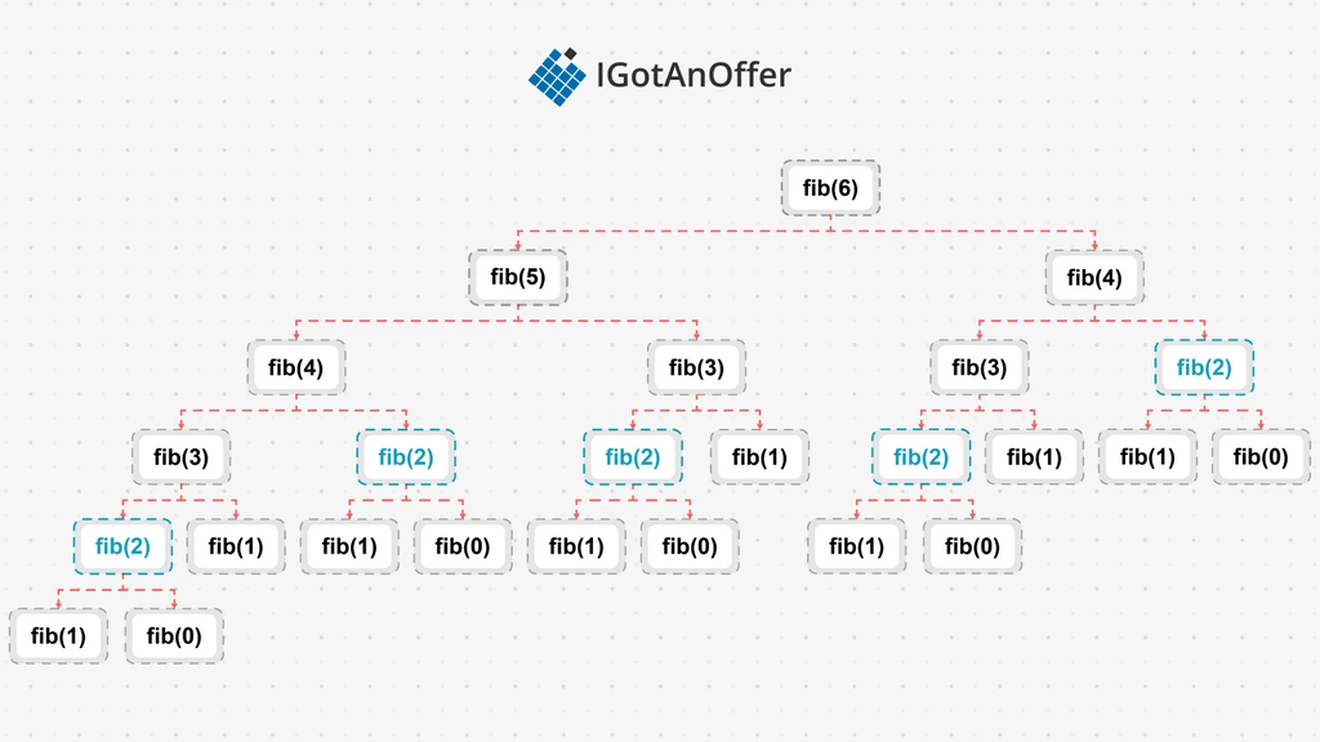
Dynamic programming allows us to reduce the complexity of the solution to polynomial time by storing the results of sub-problems for retrieval later.

4.1.1 Use cases for dynamic programming (Java, Python, C++)

Dynamic programming can be applied to common problems like:

• Fibonacci problems
• Finding if a word can be built from a set of strings
• Coin change problem: from a limited set of coins build a specified amount of change
• Min cost path problem: given a matrix of vertex costs or adjacency list of edge costs, find the path with the lowest cost to given vertex
• Assembly line scheduling
• Tile stacking / box stacking problem
• Travelling salesman problem
• Palindrome problems
• Wildcard pattern matching
• Graph coloring problems
• CYK algorithm
• Levenshtein distance
• Diff programs

4.1.2 Example implementation

There are two ways to apply dynamic programming to recursive functions: memoization, the “top-down” approach, and tabulation, the “bottom-up” approach.

Memoization involves storing the solutions to sub-problems in any key-value data structure. The general process of introducing memoization is as follows:

1. Add the base inputs to the key-value store.
2. Change the base conditions to check if the call’s inputs are in the store, and return the store value if it exists.
3. Before returning from the function, store the calculated value in the store. The key is the inputs, and the value is the calculation for the inputs.

This results in the following implementation for our Fibonacci function:

Here, memo is created with the bases of 0 and 1 in the function signature. The base condition is changed to check if n is in memo. If it is, its value will be returned. In addition, the recursive call’s value gets stored in memo. The memo is also passed down the recursive calls – which is important to remember, since it has a default value.

Instead of using recursion to calculate down to the base values, we can use iteration from the base value up to our desired values. This is the principle of tabulation, which pre-computes the solutions to the sub-problems first. The tabulation process works as follows:

1. Construct a table to store all the solutions to sub-problems.
2. Fill base conditions in the table.
3. Use iteration to populate the table.
4. Return the table item at n.

For our Fibonacci problem, this yields the following implementation:

First, tab is created to store all the solutions to sub-problems and initialized to all zeros (0). The solution for i will be at index i. The base condition 0 already has value 0, so only the base condition 1 needs to get the value 1. The iteration calculates all the solutions to the sub-problems, but uses the current solution to calculate a future solution. In other words, i = 0 will calculate fib(1) and fib(2) while i = 1 will calculate fib(2) and fib(3). Finally, the solution to the nth sub-problem is returned.

Both memoization and tabulation reduce the time complexity of this Fibonacci function to O(n), while the space complexity remains at O(n). An optimization to the tabular implementation for Fibonacci can have it store only the previous two solutions to sub-problems at a time for a constant space complexity.

4.1.3 How dynamic programming compares to other algorithms

Dynamic programming can be seen as a specialization of divide-and-conquer strategies, since divide-and-conquer requires an optimal substructure (but not overlapping sub-problems). The effect of a dynamic programming solution is usually an improved time-complexity.

Greedy algorithms are also used to solve optimization problems recursively. However, greedy algorithms are not guaranteed to be optimal and can only return a single possible solution. The trade-off is that greedy algorithms are generally faster and more space-efficient than dynamic programming solutions.

Memoization is also used in other contexts to speed up function calls for repeated inputs. These implementations can be in the form of a cache (like a web server cache for incoming requests) or a proxy (like a network proxy for outgoing requests).

5. Dynamic programming cheat sheet

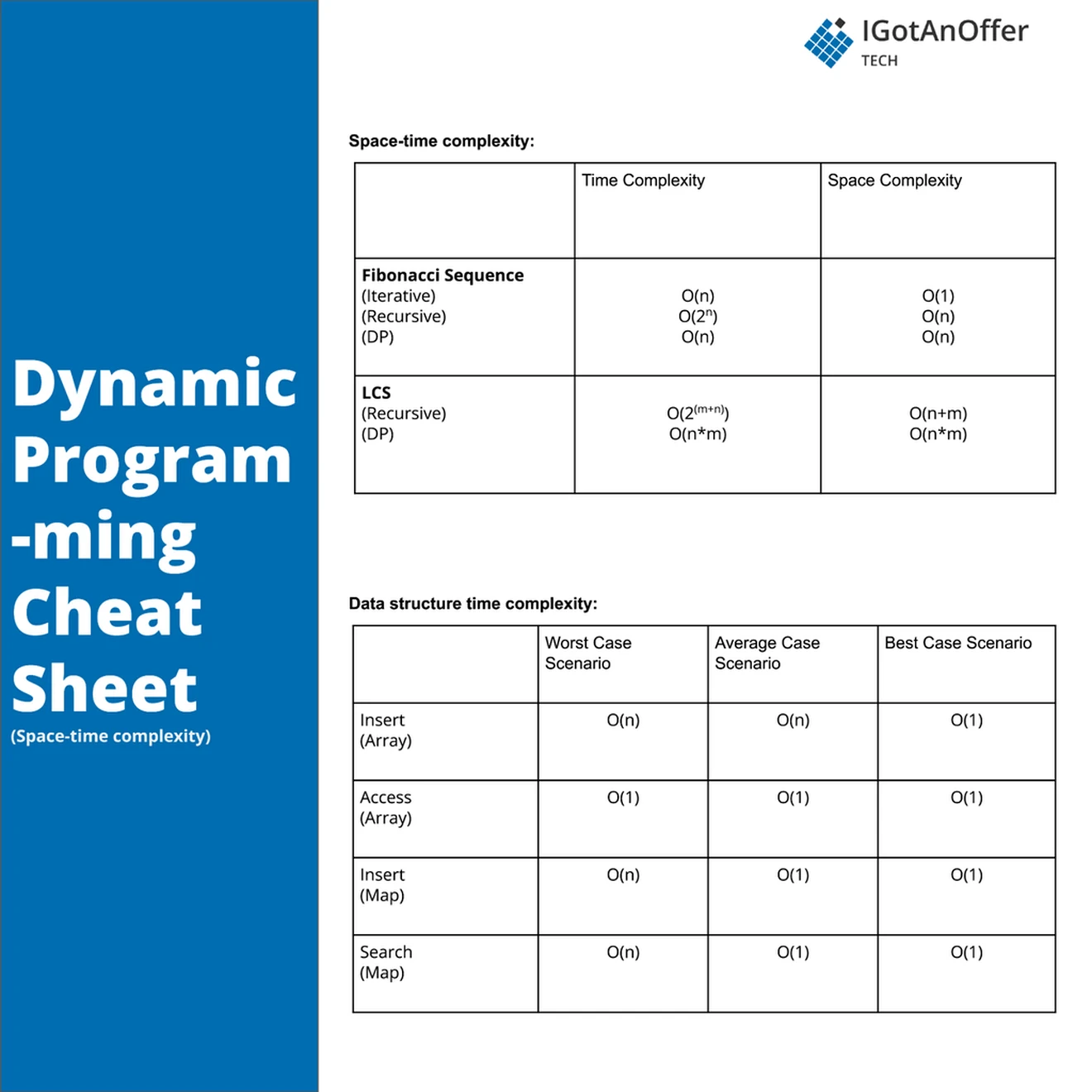
You can download the cheat sheet here.

5.1 Related algorithms and techniques

• Recursion

• Catalan Numbers

• Kadane’s algorithm

• Recursive functions

• Levenshtein distance

5.2 Cheat sheet explained

The cheat sheet above is a summary of information you might need to know for an interview, but it’s usually not enough to simply memorize it. Instead, aim to understand each result so that you can give the answer in context.

The cheat sheet is broken into time complexity and space complexity (the processing time and memory requirements for dynamic programming). Dynamic programming is related to several data structures, which are also included in the cheat sheet.

For more information about time and space requirements of different algorithms, read our complete guide to big-O notation and complexity analysis.

5.2.1 Time complexity

The non-dynamic programming, recursive implementation of Fibonacci has a stack depth of n (the n-1 recursive calls will continue until the base condition of 1 is reached) and a branching factor of 2 – one for fib(n-1) and one for fib(n-2). This gives a total time complexity of O(2^n). Recursive implementations will have a stack depth of m with a branching factor of n to give a time complexity of O(m^n), which is exponential.

The memoization implementation will initialize the memo store the first time it is called with argument n, and the computed value will be extracted from the store the next time it’s called – effectively removing the branching factor. This gives it a time complexity of O(m) only.

The tabulation implementation will only iterate for each sub-problem to also give it a time complexity of O(m). In general, the dynamic programming implementation of an algorithm has a polynomial time complexity.

The longest common subsequence (LCS) problem demonstrates these findings. The LCS problem aims to find the longest subsequence common to two input strings, for example the inputs “csdegf” and “sdbcgafa” have the following subsequence appearing in both: “sdgf.” 

A non-dynamic solution to the LCS problem will branch by trimming the first input by one character or trimming the second input by one character until one of the inputs is exhausted, giving a branching factor of 2 and a depth of n, for a time complexity of O(2^n).

A tabulation implementation of the solution has an iteration over the first input (with length i) with a nested interaction over the second input (with length j) giving a time complexity of O(i*j).

5.2.2 Space complexity

The non-dynamic implementation of Fibonacci only uses the stack space for storage. This reaches a maximum depth on the fib(n-1) tree branches, which will have a height of n-1 to give it a space complexity of O(n), which is the general case for recursive functions.

The memoization version of our Fibonacci solution also uses the stack implicitly (for a height of n), and the memo map has a maximum size of n. Our memoization implementation therefore has a total space complexity of O(n).

A tabulation solution only requires the table to store the solutions to sub-problems, which has a size of n. This implementation therefore also has a space complexity of O(n).

As a rule, a dynamic programming solution with n inputs with values of i_1, i_2, …, i_n will have a space complexity of O(i_1 * i_2 * … * i_n).

We can return to our LCS problem to demonstrate these findings too. The non-dynamic programming implementation only uses the stack when comparing input 1 (with length i) and input 2 (with length j), for a stack height of max(i, j) and a space complexity of O(max(i, j)). A tabulation implementation uses a table with dimensions of both i and j to give a O(i * j).

5.2.3 Related algorithms and data structures: hash maps, tree maps, and arrays

The memoization implementation uses a map data structure to store the results of sub-problems. Hash maps are a common key-value data structure that offer constant time insertions and lookups. Some languages have tree maps, which offer log_2 time insertions and lookups, but when both options are available, hash maps are better for memoization. At the end of the memoization implementation, the map will contain n elements to give a space complexity of O(n).

The tabulation implementation uses an array data structure to iteratively solve all the sub-problems. Arrays also offer constant time insertions and lookups. The space complexity for tabulation can vary from constant (when only a constant number of solutions to sub-problems are stored) to linear (when all the solutions to sub-problems are stored). 

6. How to prepare for a coding interview

6.1 Practice on your own

Before you start practicing interviews, you’ll want to make sure you have a strong understanding of not only dynamic programming but also the rest of the relevant algorithms and data structures. You’ll also want to start working through lots of coding problems.

Check out the guides below for lists of questions organized by difficulty level, links to high-quality answers, and cheat sheets.

Algorithm guides

• Breadth-first search
• Depth-first search
• Binary search
• Sorting
• Greedy algorithm
• Backtracking
• Divide and conquer

Data structure guides

• Arrays
• Strings
• Linked lists
• Stacks and Queues
• Trees
• Graphs
• Maps
• Heap
• Coding interview examples (with solutions)

To get used to an interview situation, where you’ll have to code on a whiteboard, we recommend solving the problems in the guides above on a piece of paper or google doc.

6.2 Practice with others

However, sooner or later you’re probably going to want some expert interventions and feedback to really improve your coding interview skills.

That’s why we recommend practicing with ex-interviewers from top tech companies. If you know a software engineer who has experience running interviews at a big tech company, then that's fantastic. But for most of us, it's tough to find the right connections to make this happen. And it might also be difficult to practice multiple hours with that person unless you know them really well.

Here's the good news. We've already made the connections for you. We’ve created a coaching service where you can practice 1-on-1 with ex-interviewers from leading tech companies. Learn more and start scheduling sessions today.